数码学堂是一个专注于数码知识教育的网站！

网站地图
首页 数码社区正文

电脑函数的最大值和最小值公式及应用（探索电脑函数的极值问题，解读极值计算方法与应用场景）

2025-07-21 10:10:56 投稿人 : 游客 围观 : 123 次 0 评论

在计算机科学和应用数学领域，函数的最大值和最小值是一项重要的研究课题。本文将介绍电脑函数的最大值和最小值公式，探讨其计算方法以及在实际应用中的意义和应用场景。

定义和概念

1.1最大值和最小值的定义：函数在某一区间内取得的最大值和最小值被称为函数的极值。

1.2极值点：函数取得极值的点被称为极值点，可以是局部极大值或局部极小值。

计算方法

2.1导数法：通过求函数导数，找到导数为零的点，判断其是极大值还是极小值。

2.2拐点法：通过求函数二阶导数，找到导数为零的点，并根据拐点性质判断其是极大值还是极小值。

应用场景

3.1优化问题：求函数的最大值和最小值可以帮助我们解决很多优化问题，如资源分配、路径规划等。

3.2机器学习：在机器学习算法中，通过寻找函数的最大值和最小值可以帮助我们找到最优的模型参数。

3.3金融分析：在金融领域，函数的最大值和最小值可以用于优化投资组合和风险管理。

数值计算和优化算法

4.1数值计算方法：对于复杂的函数，我们可以使用数值计算方法来估计其最大值和最小值，如割线法、牛顿法等。

4.2优化算法：针对函数的极值问题，研究者们发展了许多高效的优化算法，如梯度下降法、遗传算法等。

实例分析

5.1求解一元多项式函数的最大值和最小值

5.2寻找二维平面上函数的最大值和最小值

5.3应用遗传算法求解复杂函数的极值问题

极值与函数图像

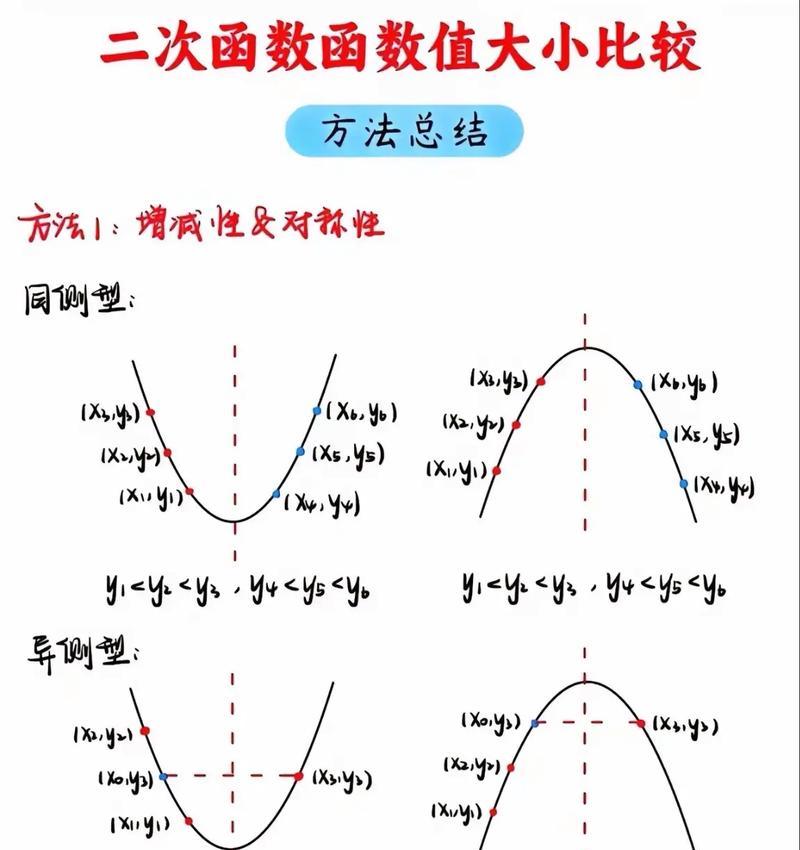
6.1极值与函数图像的关系：极大值点和极小值点在函数图像上具有特殊的形态。

6.2利用图像分析极值：通过观察函数图像，可以初步判断函数的极值点所在位置。

误差分析与收敛性

7.1误差分析：数值计算方法求解函数极值时，会产生一定的误差，需要对误差进行分析和控制。

7.2收敛性：对于一些迭代算法，我们需要关注其收敛性，即算法是否能够得到函数的真实极值。

挑战与展望

8.1多目标优化：如何求解多目标优化问题中的最大值和最小值是一个具有挑战性的问题。

8.2高维函数优化：随着数据维度的增加，函数优化问题变得越来越困难，如何有效求解高维函数的极值仍然是一个研究热点。

本文介绍了电脑函数最大值和最小值公式的定义和概念，以及计算方法和应用场景。同时还探讨了数值计算和优化算法、误差分析和收敛性等相关内容，并展望了多目标优化和高维函数优化等未来的研究方向。通过对电脑函数最大值和最小值的深入理解，我们能够更好地应用数学方法解决实际问题。

标签 ????????
上一篇：解决校园网118错误的方法（遇到校园网118错误？快来学习这些解决办法吧！） 下一篇：联想主板装机教程（一步一步教你如何使用联想主板完成装机，让你的电脑更出色）

相关文章

最近发表
推荐文章
惠普511连接电脑w7教程（详细步骤教你如何将惠普511与Windows7电脑连接）

惠普511连接电脑w7教程（详细步骤教你如何将惠普511与Windows7电脑连接）

如何使用电脑和U盘重装系统（教你轻松学会重装系统的方法）

如何使用电脑和U盘重装系统（教你轻松学会重装系统的方法）

U盘安装系统教程（从U盘中安装系统，快速、方便、高效！）

U盘安装系统教程（从U盘中安装系统，快速、方便、高效！）

随机文章
热评文章
标签列表